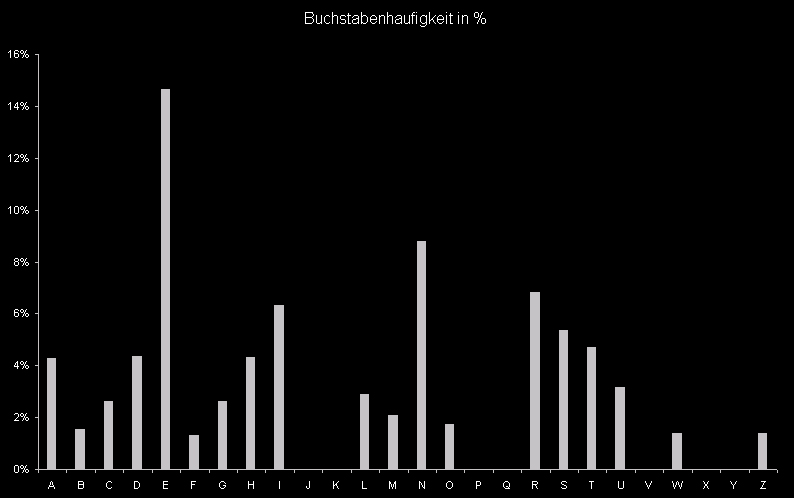
Schwachstellen: Da jedem Klartextbuchstaben ein eindeutiger Chiffrebuchstabe zugewiesen ist, ändert sich die Verteilung der H¨ufigkeiten der Buchstaben nicht. Somit ist es möglich, eine statistische Analyse vorzunehmen, anhand derer sich der Schlüssel ermitteln läßt. Das 'e' ist der häufigste Buchstabe in der deutschen Sprache (er besitzt einen Anteil von 13,17%). Um das dem 'e' entsprechende Zeichen im Chiffre zu finden, muß man also das häufigste Zeichen ermitteln - dies ist dann mit großer Wahrscheinlichkeit das 'e'. Anschließend muß man nur noch die Differenz zwischen diesem Buchstaben und dem 'e' bilden - schon hat man den Schlüssel n. Dies funktioniert desto besser, je länger der Text ist.
Bei der Buchstabenhäufigkeitsanalyse handelt es sich um ein grundlegendes Werkzeug der klassischen Kryptanalyse. Sie beruht darauf, dass die relative Buchstabenhäufigkeit in allen in einer natürlichen Sprache S verfassten Texten gleich ist. So tritt z. B. In der deutschen Sprache am häufigsten das 'e' bzw. 'E' auf, etwa 17% aller Buchstaben sind 'e's. Man kann nun die Redundanz eines Textes (d. h. ob er sinnvoll ist) durch eine solche Buchstabenhäufigkeitsanalyse überprüfen. Es wird natürlich vorausgesetzt, dass einem die Sprache, in der der Text verfasst ist bekannt ist. Umgekehrt ist es möglich, anhand der Häufigkeitsanalyse Rückschlüsse auf die Sprache eines Textes zu ziehen, ohne auf seinen Inhalt einzugehen. Probleme der Buchstabenhäufigkeitsanalyse sind kurze Texte mit evtl. großer Abweichung von den normalen Buchstabenhäufigkeiten sowie zufällige Texte, die (vielleicht absichtlich) mit der Häufigkeitsverteilung einer natürlichen Sprache versehen worden. Zu einem gewissen Grade können beide Probleme dadurch gelöst werden, dass man nicht nur einzelne Buchstaben, sondern Buchstabenfolgen (2 bis 3 Buchstaben, sog. Bi- und Trigramme sind sinnvoll) in die Häufigkeitsanalyse aufnimmt. So würden z. B. 'sch','ch', 'der', 'die', 'das', 'en', 'ei', oder 'au' sehr häufig vorkommen. Alles in allem kann die Buchstabenhäufigkeitsanalyse zwischen sinnvollen Texten und zufälligen Buchstabenketten unterscheiden, kommt gegen »fälschungen« aber nicht an. Wie viel Text-Material für die Buchstabenhäufigkeitsanalyse gebraucht wird hängt natürlich sehr von der Anzahl der zu testenden Texte ab.
